sin²ψ法の基礎式

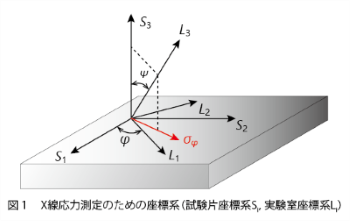
ここではsin²法によるX線応力測定に用いる基礎式についてその導出過程を紹介します。sin²法では多結晶の平面応力状態を仮定して試料の法線と試料面法線のなす角ψが異なる複数の方向の回折角2θを測定し、その結果から応力値を求めます。この測定では、試料座標系（S_i）と実験室座標系（L_i）の2つの直交座標系（図1）を考えます。試料座標系は試料上で任意に決定され、S₃は試料表面の法線となります。実験室座標系はこのX線測定系に基づいて決定され、その後、L₃方向の格子面の間隔dが sin²ψごとに測定されます。この結果を利用してS₃ 軸中心にS₁ から φ回転した方向の応力σ_φ が得られます。
このことから実験室座標系の応力テンソルは試験片座標系の応力テンソルに変換行列nをかけることで得られ、次式のように表されます
$$ \sigma_{km}^{L} = \sigma_{ij}^{S} n_{ki} n_{mj} \tag{1} $$ これをσ₃₃^Lについて展開すると次式のように表されます。 $$ \sigma_{33}^{L} = \sigma_{11}^{S} n_{31}^2 + \sigma_{22}^{S} n_{32}^2 + \sigma_{33}^{S} n_{33}^2 - 2 \sigma_{12}^{S} n_{31} n_{32} - 2 \sigma_{23}^{S} n_{32} n_{33} - 2 \sigma_{31}^{S} n_{31} n_{33} \tag{2} $$ 変換行列の具体的な中身ついて考えると、まずS₃ 軸を中心にφ回転し、続いてS₂' 軸（// L₂ 軸）を中心にψ回転するので、変換行列n は次のように求められます。
$$ n_{ij} = \begin{bmatrix} \cos\phi\cos\psi & \sin\phi\cos\psi & -\sin\psi \\ -\sin\phi & \cos\phi & 0 \\ \cos\phi\sin\psi & \sin\phi\sin\psi & \cos\psi \end{bmatrix} \tag{3} $$ 一方、ひずみε₃₃^L と応力σ₃₃^Lの関係は、フックの法則と弾性理論の不変量J₁（σ₁₁^L+σ₂₂^L+σ₃₃^L = σ₁₁^S+σ₂₂^S+σ₃₃^S）から次式のように表されます。
$$ \varepsilon_{33}^{L} = \frac{S^{hkl}_{2}}{2} \sigma_{33}^{L} + S^{hkl}_{1} \big( \sigma_{11}^{S} + \sigma_{22}^{S} + \sigma_{33}^{S} \big) \tag{4} $$ ここで、S₁^hkl ＝-ν_hkl ／E_hkl 、S₂^hkl ＝（1＋ν_hkl）／E_hklはhklに依存し、機械的な弾性定数との混同を避けるためにX線弾性定数または回折弾性定数と呼ばれます。式 (4)より次式が得られます。
$$ \varepsilon_{33}^{L} = \frac{S^{hkl}_{2}}{2} \big( \sigma_{11}^{S} \cos^2\phi + \sigma_{12}^{S} \sin2\phi + \sigma_{22}^{S} \sin^2\phi - \sigma_{33}^{S} \big) \sin^2\psi \\ + \frac{S^{hkl}_{2}}{2} \big( \sigma_{13}^{S} \cos\phi + \sigma_{23}^{S} \sin\phi \big) \sin2\psi \\ + S^{hkl}_{1} \big( \sigma_{11}^{S} + \sigma_{22}^{S} + \sigma_{33}^{S} \big) \\ + \frac{S^{hkl}_{2}}{2} \sigma_{33}^{S} \tag{5} $$ この式の右辺第1項の括弧内の3つの項（σ₁₁^S cos2ϕ + σ₁₂^Ssin2ϕ + σ₂₂^Ssin2φ）は、S₁軸からφの向きの試験片表面の面内応力成分となります。この関係から、式 (5)は次式のように書き換えることができます。
$$ \varepsilon_{33}^{L} = \frac{S^{hkl}_{2}}{2} \big( \sigma_{\phi} - \sigma_{33}^{S} \big) \sin^2\psi \\ + \frac{S^{hkl}_{2}}{2} \sigma_{33}^{S} \\ + S^{hkl}_{1} \big( \sigma_{11}^{S} + \sigma_{22}^{S} + \sigma_{33}^{S} \big) \\ + \frac{S^{hkl}_{2}}{2} \big( \sigma_{13}^{S} \cos\phi + \sigma_{23}^{S} \sin\phi \big) \sin2\psi \tag{6} $$ 平面応力状態では、面外成分応力である（σ₃₃、σ₁₃、σ₂₃）はゼロとなり、ε₃₃^Lは次式のようになります。
$$ \varepsilon_{33}^{L} = \frac{S^{hkl}_{2}}{2} \sigma_{\phi} \sin^2\psi + S^{hkl}_{1} \big( \sigma_{11}^{S} + \sigma_{22}^{S} \big) \tag{7} $$ ひずみ成分ε₃₃^Lは回折角2θを測定することによって得られ、ε = -Δ2θ / 2・cotθの関係を用いて式(7)は次式で表されます。
$$ 2\theta = S^{hkl}_{2} \tan\theta_{0} \sigma_{\phi} \sin^2\psi - 2 S^{hkl}_{1} \tan\theta_{0} \big( \sigma_{11}^{S} + \sigma_{22}^{S} \big) + \theta_{0} \tag{8} $$ この式をsin²ψで微分すると、
$$ \frac{\partial (2\theta)}{\partial (\sin^2\psi)} = - S^{hkl}_{2} \tan\theta_{0} \sigma_{\phi} \tag{9} $$ が得られ偏微分をsin²ψに対する回折角2θのグラフ("2θ-sin²ψ線図"､または単に"sin²ψ線図")として表せば、その傾きをMとして面内応力成分σ_φは 次式で求められます。
$$ \sigma_{\phi} = M \cdot K, \quad \text{where} \quad M = \frac{\partial (2\theta)}{\partial (\sin^2\psi)}, \quad K = -\frac{1}{S^{hkl}_{2} \tan\theta_{0}} \tag{10} $$

よくある質問

＊準備中
＊順次更新

X線応力測定関連の文献

・後藤徹，大谷眞一，"X線応力測定の連載講座基礎と最近の発展"，材料 47 (11), 1188-1194 (1998) | Link
・田中啓介，鈴木賢治，秋庭義明，"残留応力のX線評価－基礎と応用－"，養賢堂（2006）
・日本材料学会X線材料強度部門委員会，"X線応力測定法標準(2002年版)-鉄鋼編-"，日本材料学会（2002）
・鈴木裕，秋田貢一，"回折法による材料評価の新しい展開展　3. 中性子応力測定の新展開"，材料 58 (12), 1051-1057 (2009) | Linke
・Chapter 22. X-ray Stress Analysis, "Non-Destructive Material Characterization Methods"，Elsevier（2023）| Link